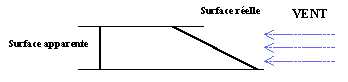
Le vent pousse la voile de notre cerf-volant. Le vent par sa pression dynamique, transmet à la voilure une force de poussée dirigée vers le haut, perpendiculaire à la surface plane du cerf-volant.

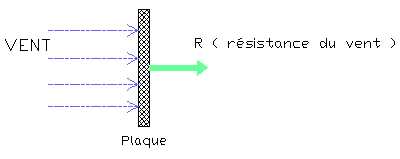
Origine de cette force de poussée ( ou résistance de l'air R ) :

Prenons un exemple, une plaque rigide maintenue verticalement à deux mains devant nous par jour de grand vent. Nous resentons une force qui nous oblige à resister. Cette force est due à la pression dynamique et est appelée communément la résistance de l'air ( R). On parle de résistance de l'air parce que cette force s'oppose au déplacement. Ainsi, on constaterait la même résistance, si un jour, par un vent de 10 km/h, on reste immobile avec la plaque et qu'un autre jour sans vent, on coure à la vitesse de 10 km/h.

Si nous réalisons la même expérience avec une plaque plus petite et une autre plus grande, nous constatons que la petite plaque ne transmet pas beaucoup de résistance alors que la grande, au contraire, transmet une forte résistance.

On notera que si la surface est vraiment perpendiculaire à la vitesse du vent (on dit aussi "normal"), la résistance de l'air s'applique au centre de gravité de la plaque.

On constate donc un principe physique selon lequel la résistance de l'air (ou du vent lorsque l'objet est immobile) est une force proportionnelle à la surface de la plaque. S'il s'agit d'un objet ayant une forme solide (un volume), la force de résistance sera proportionnelle à la surface projetée sur un plan, que l'on appelle aussi surface apparente ou parfois plus techniquement maître couple.

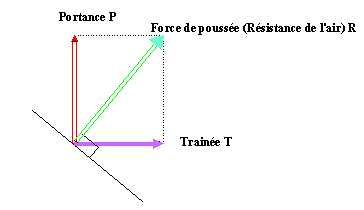
Reprenons notre expérience, par jour de grand vent, on est emporté, alors qu'au contraire par jour de vent faible, la plaque aurait tendance à tomber à terre si nous ne la maintenions pas. On constate alors par cette expérience que la force de résistance dépend de la vitesse du vent. Si l'on mesurait cette force à l'aide d'un peson par exemple ou par la compréssion d'un ressort muni d'un index se déplaçant sur une règle, on remarquerait que la résistance n'est pas proportionnelle à la vitesse du vent, mais plus la vitesse du vent est forte, plus la résistance est grande. Des expériences ont permis d'établir des relations entre les différents éléments entrant en jeu.

On a ainsi pu établir un coefficient de résistance pour le déplacement d'un objet dans l'air (appelé également coefficient de pénétration dans l'air) de formule : Cx = R/qS, dans laquelle R exprime la résistance de l'air, S la surface projetée de l'objet (maître couple), et q la pression dynamique exercée par l'air sur l'objet.

Soit R = Cx q S

On a aussi déterminé expérimentalement l'expression de la pression dynamique qui est donnée par la formule :

q = 1/2rho*V²

dans laquelle rho représente la masse volumique de l'air et V la vitese du vent.

On sait que rho = 1.25 kg/m3 à 15 °C et à pression atmosphérique normale (1015hPa), ce qui donne une expression simplifiée de la pression dynamique de l'air : q = 0.625 V²

Les forces aérodynamiques :

Nous avons vu que le vent exerce sur le cerf-volant une force perpendiculaire à la surface en un point appelée centre de poussée. Pour comprendre comment un cerf-volant peut voler, nous allons décomposé cette force en deux composantes, une composante horizontale que l'on nomme Traînée ( T ), et une comosante verticale appelée Portance ( P ).

La Traînée ( T ):

C'est une force parallèle et opposée à l'écoulement.

Lorsqu'on met en mouvement un corps dans l'air, on s'aperçoit qu'il est nécéssaire de faire un effort, non seulement lors de son accélération, mais aussi ensuite pour maintenir sa vitesse. L'air a tendance à freiner le corps pour le ramener à une vitesse nulle.

Pour se rendre compte de cette force un petit test très simple: en voiture, je passe le bras par la fenêtre et je place ma main à l'horizontale dans le filet d'air : ma main est tirée vers l'arrière, je suis obligé de faire un effort pour la maintenir en position. Elle subit une résistance au passage de l'air qu'on appelle traînée ( T ).

Si nous réalisons quelques expériences nous constatons que :

Si je roule plus vite, je sens que la traînée augmente beaucoup, et inversement si je roule moins vite, la traînée diminue beaucoup : LA TRAINEE EST PROPORTIONNELLE A LA VITESSE AU CARRE. ( V²)

Si je place ma main à la verticale, la traînée augmente : LA TRAINEE EST PROPORTIONNELLE A LA SURFACE EXPOSEE AU VENT.( S )( on appelle cette surface le maître-couple)

Si je fais l'expérience en bateau, en laissant ma main dans l'eau, pour une même vitesse, la traînée est beaucoup plus importante. Ceci est du au fait que l'eau est beaucoup plus lourde que l'air pour un même volume (1000 kg par m3^au lieu de 1.225 kg/m3 pour l'air au niveau de la mer). Par conséquent LA TRAINEE EST PROPORTIONNELLE A LA MASSE VOLUMIQUE DU FLUIDE TRAVERSEE.

Enfin si je ferme mon poing, la traînée est moins importante que lorsque ma main est à l'horizontale, alors que le maitre-couple est plus important et les autres facteurs constants. Je viens de profiler ma main, c'est à dire de lui donner une forme plus adaptée à la pénétration dans l'air. Par conséquent LA TRAINEE EST PROPORTIONNELLE A UN COEFFICIENT DE PROFIL DE L'OBSTACLE ( Cx )( coefficient de trainée).

Lorsqu'on veut profiler un corps, il faut travailler sa face avant de manière à adoucir la pénétration dans l'air et sa face arrière de manière à "recoller" proprement les filets d'air sans perte d'énergie par turbulence. Les valeurs de coefficient de traînée varient à peu près de la manière suivante :

Nous obtenons finalement l'expression de la Traînée ( T ) :

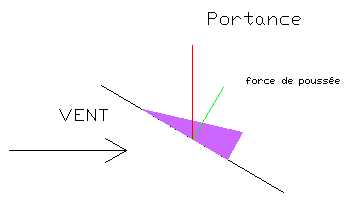
La Portance ( P ) :

C'est une force perpendiculaire à l'écoulement.

Reprenons l'exemple précedent : si maintenant j'incline ma main dans le filet d'air sans la mettre ni verticale, ni horizontale.

Une autre force apparait en plus de la traînée, perpendiculaire à la direction du déplacement et qui tend à faire monter ma main : c'est la Portance ( P ). Elle entraîne ma main vers le haut si sa position correspond à celle du schéma; si j'incline ma main dans l'autre sens, elle sera entraînée vers le bas.

On appelle l'angle que fait ma main avec l'écoulement l'incidence. Celle-ci sera comptée positivement si l'avent de ma main (coté pouce) est inclinée vers le haut, négativement dans le sens contraire. Pour le schéma j'ai choisi une incidence positive. On peut donc conclure que :

Une incidence positive amène une "portance vers le haut", soit une portance (tout simplement).

Une incidence négative amène une "portance vers le bas", soit une déportance.

Si nous renouvelons les expériences précédentes, nous constatons que la portance suit les mêmes lois de variation, c'est à dire :

LA PORTANCE EST PROPORTIONNELLE A LA VITESSE AU CARRE ( V² ).

LA PORTANCE EST PROPORTIONNELLE A LA SURFACE ( S ). Cependant, cette proportionnalité n'intervient pas par rapport au maître-couple, mais plutôt par rapport à la surface de ma main inclinée projetée à l'horizontale.

LA PORTANCE EST PROPORTIONNELLE A LA MASSE VOLUMIQUE DU FLUIDE TRAVERSEE.

LA PORTANCE EST PROPORTIONNELLE A UN COEFFICIENT DE PROFIL DE L'OBSTACLE. Mais ce n'est pas le même coefficient que pour la traînée. Il s'agit du coefficient de portance. pour chaque profil et pour chaque incidence, il va falloir calculer un coefficient de traînée ( Cx ) et un coefficient de portance ( Cz ).

Nous obtenons finalement l'expression de la Portance ( P ):

Tout à l'heure, main parallèle à l'écoulement (donc incidence nulle) et main perpendiculaire (angle incidence 90°), j'avais un Cz = 0, d'où l'abscence de portance.

D'où vient cette portance ?